7.2 Working interval

The measuring interval (sometimes called working range) is the set of values of quantities of the same kind that can be measured by a given instrument (or measuring system) with specified uncertainty under defined conditions.

In most of the analytical chemistry methods, the working interval is defined as that for which the linearity in the calibration is maintained. As mentioned in Section 6, linearity is only observed in a few specific EDXRF methods. In such cases the interval of concentrations for which the linearity is fulfilled must be assessed. The latter can be done by any of the two following approaches:

• ISO 11095 approach, the principle of which consists in comparing the residual error with the experimental error using a Fischer's test. This approach is valid for relatively narrow intervals of concentration (the measurand concentration not varying by more than a factor 10). If the counting statistics of the measurements is very high, this test becomes excessively severe. On the other hand, in the case of poor experimental conditions, the test will easily be positive and will also lose its relevance.

• ISO 8466 approach, the principle of which consists in comparing the residual error (S_y) caused by the linear regression with the residual error produced by a polynomial regression applied to the same data (see example in the figure below). If the polynomial model gives a significantly lower residual error, a conclusion of nonlinearity can be drawn. This approach is appropriate in particular when there is a risk of high experimental dispersion at any of the ends of the range, and allows defining the largest possible interval for which linearity is observed.

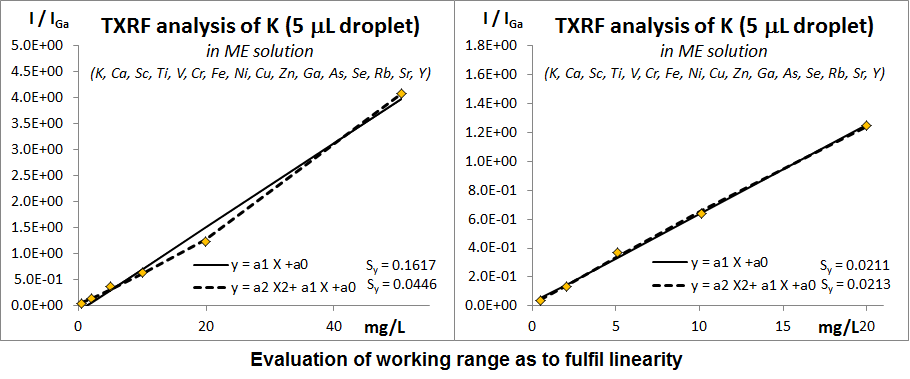
For other EDXRF methods, the interval of applicability of the model has to be assessed based on the assumptions made for the given calibration model. In the case of thin sample analysis the increase in concentration of an element can enlarge the χ_S(E₀,E_i)ρX value. For low characteristic energies the value of χ_S(E₀,E_i) must be verified for the given sample matrix and sample areal density. The presence of high concentration elements in the sample might require the use of additional corrections for enhancement effects in fundamental parameter based methods.

References:

ISO 11095:1996. Linear calibration using reference materials.

ISO 8466-1:1990. Water quality -- Calibration and evaluation of analytical methods and estimation of performance characteristics - Part 1: Statistical evaluation of the linear calibration function.