6.3.3 Influence coefficients
The concept of influence coefficients has been widely used in the literature in relation with different methods aimed at correcting the inter-element effects.
It is assumed that the concentration for any element wi can be calculated from the measured intensity Ii, which has an influence from the matrix Mi and some background signal Bi, and can be represented as
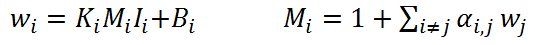
The alpha coefficients are supposed to reflect the influence of the N elements j present in the sample (either attenuation or enhancement) The values of the coefficients αi,j, the sensitivity Ki and the background Bi can be found in empirical algorithms from the measurement of reference materials with varying combinations of the concentrations of the elements and covering the expected interval of concentration.
Lachance and Traill proposed in 1966 an algorithm that can be derived from the Sherman formula for infinitely thick samples in the case of monochromatic excitation and if enhancement effects can be neglected.
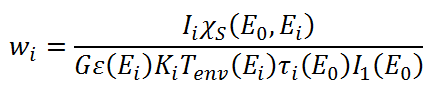
The sample attenuation coefficient can be re-written as
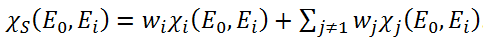
If the sum of the concentration of all elements equals 1, then
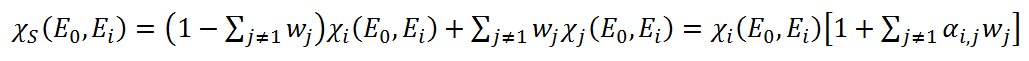
where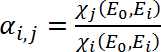 
Therefore
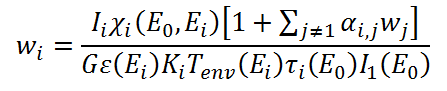
And if we replace the value of χi(E0,Ei) by deriving it from the Sherman equation for the pure element:
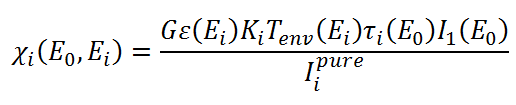
Then we obtain the formula of Lachance-Traill:
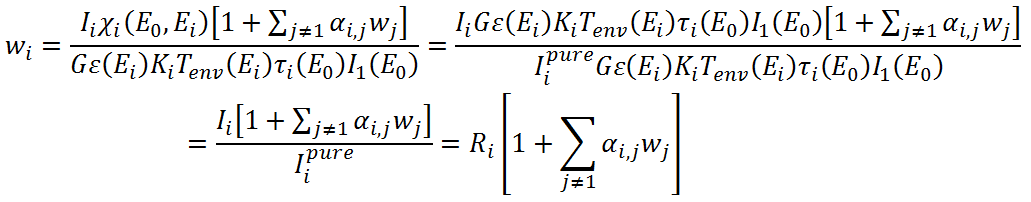
where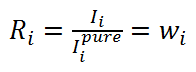 
The coefficients can be theoretically calculated as
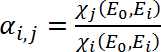for a given instrumental arrangement, but it is worth to highlight that such formula is derived only for the case of monochromatic excitation and for thick samples.
The method has two main disadvantages: The number of required standards for empirical calibration is very large and; the presence in the sample of any element having large concentration and not being included in the calibration model (e.g. non-detected elements) can lead to significant errors in the results.
IAEA QXAS include the program "NBS alpha coefficients", which can be accessed from the initial Menu option "Quantitative analysis" to implement a calibration following this approach.
Reference: Lachance, G.R.; Traill, R.J., A practical solution to the matrix problem in X-ray analysis, Canadian Journal of Spectroscopy, 11 (1966) 43