6.1.3 Thin samples

Thin samples are the easiest case for quantification. If the product 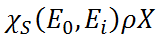has a small value, e.g. 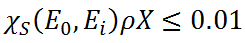then the exponential factor in the attenuation correction can be replaced by its approximation using a Taylor series:

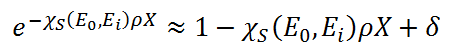
Then the attenuation correction no longer depends on sample matrix but only on sample areal thickness ρX

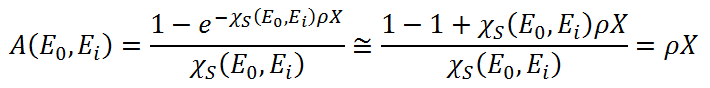
And the intensity of measured counts is linearly proportional to the elemental areal density:

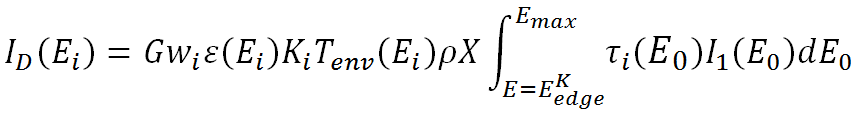
Or for the case of monochromatic excitation becomes

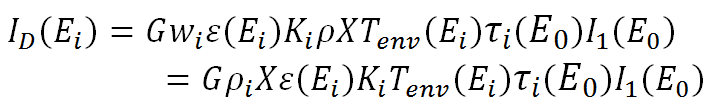
It has to be understood that the classification of sample thickness strongly depends on the energy of the fluorescence radiation. While many samples might be thin for the excitation radiation energy, the condition of thin layer must be verified for the analytical lines, especially for low energy ones.